引子

这个方法是原来乱翻线代书(Linear Agebra Done Right)看到的，当时就觉得非常厉害，但由于要求积分，一直不知道怎么实现。现在好了，多项式学了， Simpson 自适应积分也会了。闲来无事填个坑。

定义

  • \(V\)为所有\(f(x):\mathbb{R}\to\mathbb{R}\)组成的集合
  • 对\(u,v\in V\)，定义其内积(Inner Product)为

\[ <u,v>=\int_a^b{u(x)v(x)dx} \]

\((a,b)\)就是给定的区间啦

  • 对\(u\in V\)，定义其模(Norm)为

\[ ||u||=\sqrt{<u,u>} \]

  • 对于\(V\)中一组向量(也就是元素)\((u_1,u_2,\ldots,u_n)\)，我们称它为一组基，当且仅当，\(\forall v\in V\)，存在唯一的\(a_1,a_2,...,a_n\in R\)，使得

\[ v=a_1u_1+a_2u_2+\ldots+a_nu_n \]

  • 对于一组基\((u_1,u_2,\ldots,u_n)\)，我们称它为正交的，当且仅当

\[ <u_i,u_j>=0,\forall i,j \in\{1,\ldots,n\} \]

  • 对于一组基\((u_1,u_2,\ldots,u_n)\)，我们称它为单位基，当且仅当

\[ <u_i,u_i>=1,\forall i \in \{1,\ldots,n\} \]

性质

  • 内积\(<u,v>=\int_a^bu(x)v(x)dx\)，\(a<b\)满足

    1. 交换律:

      \(<u,v>=<v,u>\)

    2. 线性:

      \(<u+v,w>=<u,w>+<v,u>\)

      \(<ku,v>=k<u,v>, k\in \mathbb{R}\)

    3. (非负性?忘了怎么说了):

      \(<u,u>\ge 0\)

      (因而\(||u||\)总是有意义的)

  • 若\((u_1,u_2,...,u_n)\)为一组单位正交基，则\(\forall v \in V\)，有

\[ v=<v,u_1>u_1+<v,u_2>u_2+\cdots+<v,u_n>u_n \]

Proof:

由\((u_1,u_2,\ldots,u_n)\)为一组单位正交基，设\(v=a_1u_1+a_2u_2+\cdots+a_nu_n\)，两边同时与\(u_i\)内积即有

\[ <v,u_i>=<a_1u_1,u_i>+<a_2u_2,u_i>+\cdots+<a_nu_n,u_i> \] \[ =a_1<u_1,u_i>+a_2<u_2,u_i>+\cdots+a_n<u_n,u_i>=a_i \]

应用

假如\((x^0,x^1,x^2,...)\)为\(V\)的一组基的话，我们就可以把任何一个函数写成\(\sum{a_ix^i}\)的形式了，诶诶诶，这不就是我们想干的事嘛，用多项式来表示函数。

那么问题来了，我们该怎么求那个系数\(a_i\)？

不妨假设，我们求出了一组单位正交基\((u_1,u_2,\ldots)\)，对其中每个 \(u_i\)，它表示成\(\sum{a_ix^i}\)形式的系数都是已知的，那我们岂不是可以先求出用\((u_i)\)表示的系数(利用刚才提到的内积)，再回代就可以得到用(\(x_i\))表示的系数。

那么我们只需要求正交基即可。

下面就直接给出算法了。

设已经有了一组单位正交基\((u_1,u_2,\ldots,u_n)\)，\(v\)不能被\((u_1,u_2,\ldots,u_n)\)表示，设

\[ t=v-<v,u_1>-<v,u_2>-\cdots-<v,u_n> \]

则

\[ u_{n+1}=\frac{t}{||t||} \]

\((u_1,u_2,\ldots,u_n,u_{n+1})\)的单位性与正交性很好验证。而且原来\((u_1,u_2,\ldots,u_n,v)\)能表示出来的元素\((u_1,u_2,\ldots,u_n)\)都能表示。

所以就完啦～

例子

\[ f(x)=sin(x) \]

与

\[ g(x)=0.987862x-0.155271x^3+0.00564312x^5 \]

的函数图像画在一起,可以看到两者在\((-\pi,\pi)\)上十分重合。

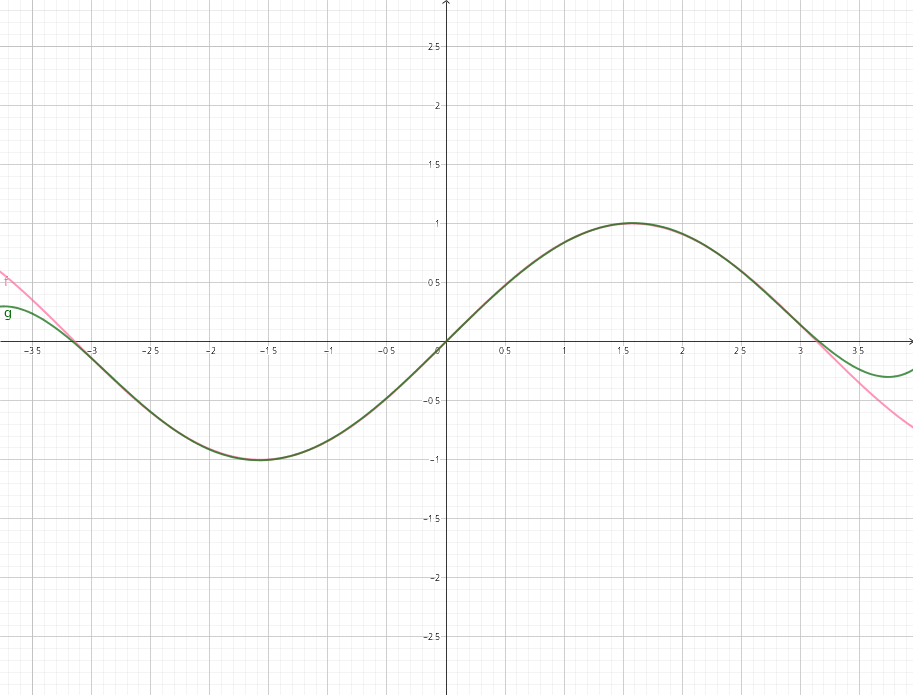
粉色为f(x)，绿色为g(x)
粉色为\(f(x)\)，绿色为\(g(x)\)

我们仅需用很少的项就可以实现较高的精度。(比泰勒展开不知道高到哪里去了)

实现

有点丑，不过能用。(需开启C++11)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<iostream>
#include<algorithm>
#include<functional>
#include<cmath>
#include<complex>
using namespace std;
typedef double db;
typedef function<double(double)> func;
typedef complex<db> C;
const db eps=1e-10;
const int N=1e6;
db A,B; // 积分上下界
struct poly_t {
	db a[32];int deg;
	db operator()(db x) const{
		db ret=0;
		for(int i=deg;i>=0;i--) {
			ret=ret*x+a[i];
		}
		return ret;
	}
	void init() {
		deg=0;fill(a,a+32,0);
	}
	poly_t& operator += (const poly_t &o) {
		deg=max(deg,o.deg);
		for(int i=0;i<=deg;i++)
			a[i]+=o.a[i];
		return *this;
	}
	poly_t& operator *= (db k) {
		for(int i=0;i<=deg;i++) a[i]*=k;
		return *this;
	}
	poly_t& operator /= (db k) {
		*this*=1.0/k;
		return *this;
	}
	poly_t& operator -= (const poly_t &o) {
		deg=max(deg,o.deg);
		for(int i=0;i<=deg;i++)
			a[i]-=o.a[i];
		return *this;
	}
	poly_t() {init();}
	void Print() {
		for(int i=0;i<=deg;i++)
		printf("%lf ",a[i]);puts("");
	}
};
db calc(db l,db r,const func& f) {
	return (r-l)/6*(f(l)+4*f((l+r)/2)+f(r));
}
db Simpson(db l,db r,const func& f) {
	db mid=(l+r)/2,
	left=calc(l,mid,f),
	right=calc(mid,r,f),
	whole=calc(l,r,f);
	if(fabs(left+right-whole)>eps)
	return Simpson(l,mid,f)+Simpson(mid,r,f);
	else return whole;
}
db InnerProduct(const func& u,const func& v) {
	return Simpson(A,B,[u,v](db x){return u(x)*v(x);});
}
poly_t base[6];
int main() {
	int i,j,k;
	const db Pi=3.1415926535897932384626433832795;
	db alpha;
	poly_t tt;
	A=-Pi;B=Pi;
	for(i=0;i<6;i++)
		base[i].a[i]=1,base[i].deg=i;
	for(i=0;i<6;i++) {
		for(j=0;j<i;j++) {
			tt=base[j];
			alpha=InnerProduct(tt,base[i]);
			tt*=alpha;
			base[i]-=tt;
		}
		base[i]/=sqrt(InnerProduct(base[i],base[i]));
	}
	poly_t ans;
	func origin=[](db x){return sin(x);};
	for(i=0;i<6;i++) {
		tt=base[i];
		alpha=InnerProduct(origin,tt);
		tt*=alpha;
		ans+=tt;
	}
	ans.Print();
}